9-14-2023 -Update - I'm updating the math formulas to fit a 40 ton payload of capacitors, it seems to work out...waiting for feedback from engineers...also DONT FORGET about CPA method of lasers!!

Directed Energy Weapons, Specifically Laser Capabilties

What is the Ideal Laser Frequency to Cause Fires and damage to metal and biological materials?

Energy Range: Approximately 1.65 eV to 3 eV.

eV is “electron energy distribution”

Fires: Concentrated visible light, such as from focused sunlight or powerful lasers, can ignite flammable materials.

Metal Melting: Typical visible light doesn't melt metals, but high-intensity lasers in the visible range can provide localized heating and melting.

Can a Satellite ignite a fire from space?

Yes.

Here's a simplified analysis, with variables that affect laser energy:

Atmospheric Absorption and Scattering: The Earth's atmosphere will absorb and scatter some of the laser energy. Depending on the specific wavelength, certain parts of the electromagnetic spectrum can be absorbed by water vapor, carbon dioxide, and other atmospheric constituents. The laser would need to be in a wavelength range that minimizes this absorption and scattering. The longer the path through the atmosphere, the more significant this effect becomes.

Beam Divergence: The laser beam will spread out or diverge as it travels. A laser with a very small beam divergence is essential to ensure that the beam remains focused over the long distance from the satellite to the Earth's surface. Advanced optics would be required.

Energy Intensity: To ignite a material, the laser's energy intensity (energy per unit area) must be above a certain threshold. The type of material, its moisture content, and other factors will dictate the ignition energy required.

Laser Duration: Prolonged exposure would likely be needed, especially if the initial energy intensity is near the threshold for ignition. This would mean the satellite would need a way to keep the laser fixed on a single point for an extended period, which is challenging due to the satellite's movement.

Given these variables, a rough estimate of the energy:

For simplicity, let's assume:

The laser's energy is mostly in the red to near-infrared range (closer to 1.65 eV), which might have better transmission through the atmosphere than violet.

We're trying to ignite dry paper, which has an ignition energy of roughly
1×10^7 W/m².

Learn about Ignition Energy here

If you can focus the laser into a 1 cm² spot on the paper (a relatively large spot for such a distance), the power required is
1 × 10^7 W/m² * 0.0001 m² = 1000 W or 1 kW.

You would need a much more powerful laser on the satellite, perhaps on the order of several tens or even hundreds of kilowatts.

How long would it take a 10 Megawatt laser to burn a 1cm^2 piece of paper?

Let's attempt to analyze this hypothetical situation.

Laser and Its Wavelength: A laser with an energy of 1.65 eV corresponds to a wavelength of about 750 nm, which is in the near-infrared (NIR) range. Paper is more transparent to NIR than visible light, so it would not absorb the energy as efficiently as it would with a visible wavelength.

Distance and Divergence: A significant problem is the distance and divergence. Satellites can be hundreds to tens of thousands of kilometers away from the Earth's surface. Even with highly collimated laser beams, they will diverge over large distances. This divergence reduces the power density (Watts per square meter) of the beam, making it less effective.

Atmospheric Interaction: As the laser beam travels through the atmosphere, some of the energy will be absorbed and scattered, further reducing the beam's intensity.

Energy to Ignite Paper: It takes approximately 16-21 MJ/kg to ignite paper, and paper has a density of roughly 800 kg/m^3. A standard sheet of paper is about 0.1 mm thick and weighs about 5 grams (0.005 kg). If we simplify and consider just the energy to ignite (not necessarily sustain burning), it would need

E=0.005×16×10^6

E=80,000J

Assuming 10% of the 10 MW laser's energy effectively reaches and is absorbed by the paper.

That's 1 MW or 1×10^6 Watts.

Time to Burn:

t = E / Power

t = 80,000 / 1 x 10^6

t = 0.8 Seconds

It would take 0.08 seconds to burn the paper.

How long would a 10 megawatt laser in the 1.65 eV range Orbiting Earth Have to pulse to cause a 1 mile long fire?

Creating a Fire from a Laser beam on a satellite has many factors including the material being ignited, moisture content, atmospheric conditions, laser focusing mechanisms, and the energy distribution of the laser on the ground. Here, is a very simplified analysis:

Atmospheric Absorption and Scattering: The laser beam will undergo absorption and scattering as it passes through Earth's atmosphere. This means not all of the 10 MW will reach the surface.

Beam Divergence and Distribution: For a mile-long fire, the beam would need to be distributed over a long area. If you had a continuous beam, it would be spread very thinly over that distance. Alternatively, a pulsed laser could potentially scan the mile-long area in segments. i.e. a moveable beam focus would scan by moving Left to right, up, then right to left, up, repeat.

Ignition Energy: The energy required to ignite material on the ground varies. Dry grass, for example, would ignite more easily than wet wood. For a rough estimate, let's consider the ignition energy of dry grass to be around

2 ×10^6 W/m^2

The time estimate would be:

Laser Power and Area Coverage: Assuming, after all atmospheric losses, that 50% of the laser's power (5 MW) reaches the ground. If this power is focused on a 1 m^2 area, its energy intensity would be 5 MW/m^2. This is more than enough to ignite dry grass almost instantly.

Time Calculation: If the laser is pulsed and scans a mile-long area in segments (let's say 1 m^2 segments), then for a 1-mile x 1 m strip:

Total area=1 mile×1 m=1,609.34 m^2

If each 1 m^2 segment is ignited almost instantly, then the time to ignite the entire strip would depend more on the time to scan or switch between segments rather than the ignition time itself.

For this scenario, if the laser has an advanced targeting system that can pulse and move to the next segment in 0.1 seconds (a very fast, but theoretically possible speed for a high-tech laser system), then:

Total time=1,609.34×0.1 seconds=160.934 secondsTotal time=1,609.34×0.1 seconds=160.934 seconds

So, roughly 161 seconds or about 2.7 minutes to scan and ignite the entire mile-long strip.

How much energy is required for a 10 megawatt laser to pulse for 161 seconds?
How many capacitors would be required and how heavy would they be?

Breaking down the problem step by step:

Energy Required by the Laser: The energy E required by a 10 MW laser to pulse for 161 seconds is given by:

E=Power×Time

E=10 MW×161 seconds

=1,610 MWh=1.61×109 WhE

=10 MW×161 seconds

=1,610 MWh

=1.61×109 Wh

Energy Stored in a Capacitor: The energy E stored in a capacitor is given by:

E=(1/2)CV^2

Where:

C = Capacitance of the capacitor (in Farads)

V = Voltage across the capacitor (in Volts)

For the sake of an example, let's assume we're using a high-energy capacitor like those used in some advanced projects or labs. Suppose one such capacitor has a capacitance of 1 Farad and is rated for 1,000 Volts. Then the energy stored in one capacitor would be:

E=1/2 × 1F × (1,000 V)^2

=500,000 Wh

=500 kWhE

Number of Capacitors Required:

Number of capacitors=Total Energy Required / Energy per Capacitor

Number of capacitors=1.61×10^9 / 500,000 Wh

=3,220 capacitors required

Weight of the Capacitors: Assuming each capacitor weighs approximately 10 kg (a rough assumption, as the weight of capacitors can vary greatly based on their design, materials, and manufacturer),

the total weight would be:

Total Weight=3,220 capacitors×10 kg/capacitor

=32,200 kg Total Weight

So, you would need 3,220 capacitors with a total weight of 32,200 kg.

What Kind of Payload Weights Can China Put Into Orbit?

Chinas most powerful rocket (March 5 family of rockets) can launch 48,500 kg’s

How long would it take a 1.65 eV laser with 10 megawatts to liquify an aluminum allow car wheel from a satellite?

Let's Break this down step by step. There are many complex considerations, including the energy absorption properties of aluminum, atmospheric interference, and the laser's divergence over long distances. This will be a high-level , rough approximation.

Laser Properties: A 1.65 eV laser is in the near-infrared range, roughly around 750 nm in wavelength. Aluminum reflects a significant amount of this wavelength, meaning the material won't absorb the energy efficiently.

Wheel Properties:

Melting point of aluminum: Around 660.32 Celsius (or 933.47 K).

Specific heat of aluminum: 903 J/kg*K

Latent heat of fusion for aluminum: 397 kJ/kg

Assuming the aluminum alloy wheel weighs around 9 kg. This is a ballpark figure; real values may vary based on the wheel's size and design.

Energy Required to Heat the Wheel:

E1 = Mass × Specific Heat × Temperature Difference

Assuming the wheel starts at room temperature, 25 C or 298.15 K

E1=9 kg×903 J/kg*K × (660.32−25)

E1 ≈ 5.2 MJ

Energy to Melt the Wheel:

E2 = Mass × Latent Heat of Fusion

E2 = 9 kg × 397,000 J/kg

E2 ≈ 3.6 MJ

Total Energy Required:

E = E1+E2

E ≈ 8.8 MJ

Laser Efficiency and Atmospheric Interference:

Let's optimistically assume that 10% of the 10 MW laser's energy effectively reaches and is absorbed by the wheel due to atmospheric scattering, beam divergence, and the reflectivity of aluminum.

Thus, effective power = 0.1×10 MW, or 1 MW.

Time to Melt:

t = E / Power

t = 8.8 MJ / 1 MW

t ≈ 8.8 seconds

With the optimistic assumptions and simplified scenario, it would take approximately 8.8 seconds to melt the aluminum alloy wheel with a 10 MW laser from a standard satellite orbit range.

Most likely severe fire temperatures could also cause liquification of aluminum allow car wheels

Is a 1.65 eV or 754 nm Laser Visible to the human eye?

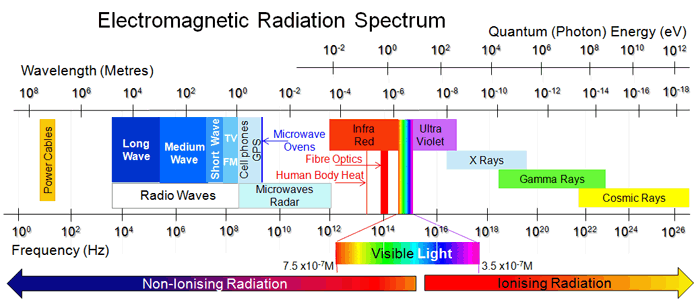
You can't see or feel near-infrared light. Far-Infrared light, however, is thermal, and although we can't see it, we can feel it through the sun, a campfire, your radiator, or the hot summer pavement. A 754 nm laser falls in the near-infrared (NIR) range and is just beyond the red end of the visible spectrum. The typical human eye perceives wavelengths from about 400 nm (violet) to roughly 700 nm (red). While 754 nm is beyond this range, some individuals may faintly perceive extremely bright sources close to the red end, but generally, it's considered outside of the visible range for most people.

So, while a 754 nm laser emits light in the near-infrared range and is not visible under standard conditions, under very intense emission or in specific situations, there might be a faint red glow perceivable at the edge of human vision. However, this isn't typical, and it's crucial to remember that looking directly at a laser, even if it's not visible, can be harmful to the eyes. Always exercise caution when working with or around lasers.

Was there a Satellite Flying above Maui at the time of the Fires?

Yes. NORAD tracks all space objects The Object in this Video is NORAD_ID=57288, known as "OBJECT A", launched by the CCP

Here is my Source Code...yes, it's only 8 lines of MatLab Script

%MatLab version R2023a

%Need Aerospace Toolbox, and Aerospace Blockset Add ons

% file name 57288.txt with TLE data :

% CCP-"OBJECT A" NORAD_CAT_ID=57288

% 1 57288U 23095A 23238.88607862 .00000048 00000-0 60389-4 0 9994

% 2 57288 86.5074 359.5870 0018551 160.6773 199.5077 13.40116728 6499

tleFile='57288.txt';

startTime = datetime(2023, 8, 7);

stopTime = datetime(2023, 8, 10);

sampleTime = 60;

sc = satelliteScenario(startTime,stopTime,sampleTime);

sat1 = satellite(sc,tleFile);

elements1 = orbitalElements(sat1);

%Play Satellite Scenario

play(sc);

Here is the CCP-"OBJECT A" Satellite Orbit Propogation on August 8th, 2023 in Maui Using MatLab and standard tools listed above

9-1-2023 Update, I have found 8 objects over Maui at the time of fires on 8-8-2023.

I have found out that the Chinese CCP March Lineup of Rockets can power a ~70 +/- GigaWatt NIR Laser. I'll be publishing more data soon. Please follow me on Gab Social @Subvertio, Truth Social @Subvertio for the latest updates. Twitter Banned me from ads and I filed a small claims case against them to refund my ad money. Elon Musk IS NOT running a Free Speech Platform-Don't trust him. Tesla is over valued, Twitter isn't Free Speech, Neural Link will Fail, and the next Starship launch will blow up too. He's running off of "Bot Hype" on twitter/x and nothing tangible as I have put 120k miles on a Tesla Model S and I'll never have an electric car again after how bad it performed and being towed 3 times. More updates coming soon, please follow me!

9-1-2023 Update, 10 Petawatt Laser that fits on a table from China, I suspect I'm grossly UNDER calculating capable laser energies as of 2023

Source - https://www.alphr.com/science/1008390/china-super-laser/

Chirped Pulse Amplification (CPA) was developed by Donna Strickland and Gérard Mourou in the mid-1980s, for which they later received the Nobel Prize in Physics in 2018. CPA is a technique that involves stretching an ultrashort pulse of light in time (making it "chirped"), amplifying it, and then recompressing it. The stretching process is essential because it reduces the pulse's peak power during the amplification stage, preventing damage to the amplifying medium. Once the stretched pulse is safely amplified, it is recompressed to produce an ultra-high-power, ultra-short pulse of light.

9-4-2023 Update Space Force 75th, nerd warriors may blow sh*t up

Source - https://www.space.com/space-force-1st-targeting-squadron

I don't believe for one second that Oprah, Bezo's or other elites would have the power to Zap Maui...The simplest explanation is Foreign Satellites...Specifically the CCP with large payload capacity rockets and powerful laser technologies. I suspect Space Force is about to blow up a bunch of mystery satellites WITH GOOD CAUSE. I'm publishing all the CCP crap I found above Maui at the time of fires soon within next couple of days.

9-5-2023 Update Final Satellite Data Published

MisterRobots.com <-Front Page

I found 2 Satellites with potential Directed Energy Capabilities that were over Hawaii at the EXACT time of the three major Fires, Please See Video on Front page. NORAD Satellite Catalog ID 53299 passes TWICE at the exact time of Kula & Olinda Fires. NORAD 55836 passes over the time of the Lahaina Fires. Please Share this information and follow me on Truth Social @Subvertio and Gab Social @Subvertio. I'll be publishing the source code soon that any kid can validate with Matlab.